Recently I’ve been reading about how to approach representation for 2D shapes. I’m curious since, as an 2D artist, we use shapes to build up characters, objects, scenes, compositions, and they seem to be the building blocks of the resulting image. I wonder what kind of representations/data structures we can use to store shape information.
Here’s a list of existing methods that I found (so far):
- Represent the contour of a shape as curves, with usual curve representations like Bezier Curve, NURB, B-spline, etc.
- Use an image crop of the shape as a template (and can compare shapes with distance function like Chamfer distance)
- Shape context: first sample points on the contour of the shape, then use the distribution of relative positions of the points as the representation.
- Conformal mapping: model each shape as a transform from a unit circle.
- Fourier Descriptor: decompose the contour of the shape into contours of different frequency.
- Implicit fields / level set: find a function \(f(x)\), where \(x\) is coordinates on the input image, such that \(f(x) = c\) correspond to the target contour (\(c\) is a constant).
In this post I wanted to focus on an implementation for implicit fields. As one might have guessed, we’re using a neural network for \(f(x)\). Specifically I implemented the implicit fields decoder proposed in this paper (there are a few other papers proposing similar ideas around the same time, such as the Occupancy Networks and DeepSDF). I chose to implement this one since the formulation is rather simple, and the shape interpolation examples the author provided look really nice.
In this paper, the implicit fields formulation is used as a decoder of an autoencoder. A shape is first encoded into a vector \(v\), then the decoder function takes in the image coordinates \(x\) and the code \(v\), and outputs a single value indicating whether the coordinate \(x\) falls inside (1) or outside the shape (0). Since the output is binary, a binary cross entropy loss is applied.
The paper mentioned a few 2D examples but focuses more on 3D shapes. I only implemented the 2D use case, however should be straightforward to apply to 3D. My Tensorflow implementation for the decoder can be found here, the training script here, with configurations here.
For a batch of MNIST digits input:

The autoencoder output:

I’m especially curious to try out shape interpolation. Interpolating from a 9 to a 4:

Interpolating from a 0 to a 1: (the intermediate images look slightly like a 3)
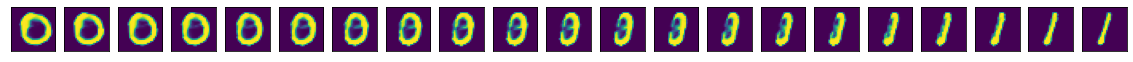
The paper also proposed using the decoder as the generator in a GAN for generating shapes. Perhaps something I’ll try for another post. A few closing thoughts about this representation:
- It’s nice that one can control the dimension of the representation, and that all shapes have the same number of dimensions (unlike representing as curves, where different shapes can have different number of control points).
- Interpolating the latent code gives a somewhat intuitive interpolation of the resulting image.
- To train/use the decoder, we need to input the coordinates of the location of the contour/boundary, and the areas nearby. For an arbitrary code, it’s not straightforward to find where that would be. For 28x28 images like MNIST it’s ok to pass in all coordinates, but for larger images this isn’t very feasible.
