Continual learning has always been an interesting topic to me. We as humans learn in a dynamic environment that’s constantly changing, but we have no trouble retaining our learnings from past examples and use it on new examples. In contrast, a deep network tends to optimize towards the current samples, but there’s no mechanism/incentive for it to retain what it has learned before. Therefore, when the training data distribution shifts away and we test the network on previously seen samples, the network often performs poorly, which is called catastrophic forgetting.
In recent years, there are lots of work trying to alleviate this problem, by either constraining the weights change from task to task, assigning parts of the network to each task, remembering and replaying past samples, etc. Most of this line of work focus on improving catastrophic forgetting, and the evaluation is made on testing on previous seens tasks.
This formulation somewhat bothers me, since - well, we don’t know if it’s good to remember past samples. As the network likely only has limited learning capacity, retaining knowledge from past tasks might hinder learning future tasks, which might be more important. In addition to being able to remember previous tasks, we might also want to be able to know what to remember and what to forget.
Another line of work, meta learning, aims to be able to quickly learn a new task. For MAML-like algorithms, it learns an initialization of the network weights that can get to lower loss over only a few training steps. In Learning to continually learn, a MAML-inspired algorithm is proposed to learn to remember past tasks (the loss function include samples from previous tasks). A “neural modulating network” is used for remembering - it’s a separate network that outputs a mask to the activation of prediction network, and therefore masking the forward pass output and also the backward pass gradient.
A more recent work OSAKA proposes to change the continual learning setting. Instead of seeing a sequence of tasks and being tested on all tasks at the end, the tasks are sampled over time. Specifically, every time a task is finished, there’s probability \(\alpha\) that the same task will be repeated. Otherwise, a new task is sampled from the task repository. The performance of the network is evaluated as the sum of loss over training. So, the network should learn new tasks quickly, and also remember/re-learn previously seen tasks quickly (however note that in their actual implementation it’s almost impossible to see an exact same task as before, once switched to a different task).
Combining these ideas, I wanted to see if one can apply the masking strategy to handle the evaluation scenario in OSAKA.
Before getting into a complex setting, as a preliminary experiment, I first test my code on a simple dataset. I created a synthetic dataset containing 2D points sampled from two Gaussian distributions, and assign them to two class labels:
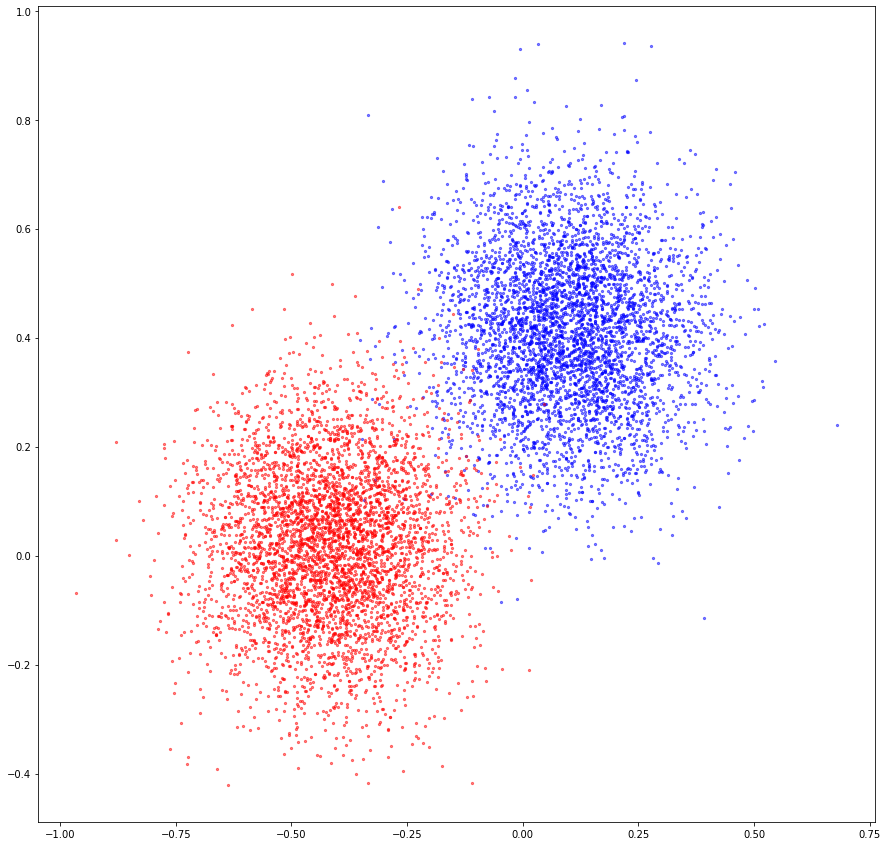
The two classes are treated as two tasks and are seen sequentially.
On the architecture side, I have two networks - one (inner network) outputs two class probabilities, and the other (meta network) outputs a mask to the second to the last layer of the prediction network.
The inner network runs in an inner loop: for every epoch, the weights are initialized, and trained for all the data points with classification loss. The meta network runs in an outer loop: the weights are only initialized before the first epoch, and the loss is the sum of the inner network loss over a sliding window. The sliding window is used to approximate the sum of loss over time - since one epoch has many inner training steps, it’s computationally unrealistic to have the meta network look at all losses over the whole epoch.
First we see if the meta network is learning correctly:
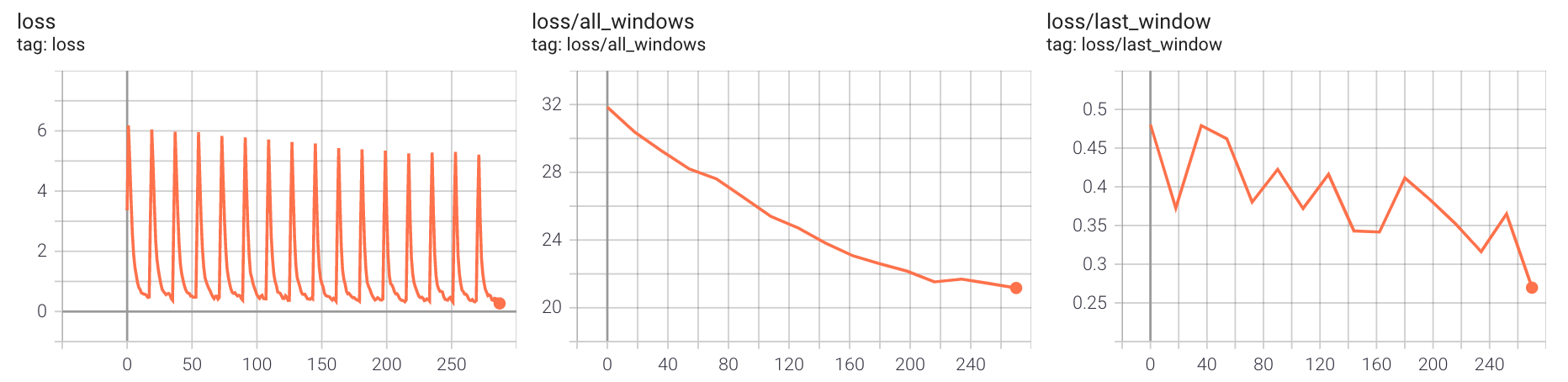
We can see the loss over time seems periodic - this is normal as each peak corresponds to the starting of a new epoch, where the inner weights are re-initialized and the loss is high. From the second and the third plot we see that the overall loss and the final loss are indeed going down.
Does the meta network learn any interesting masking strategy?
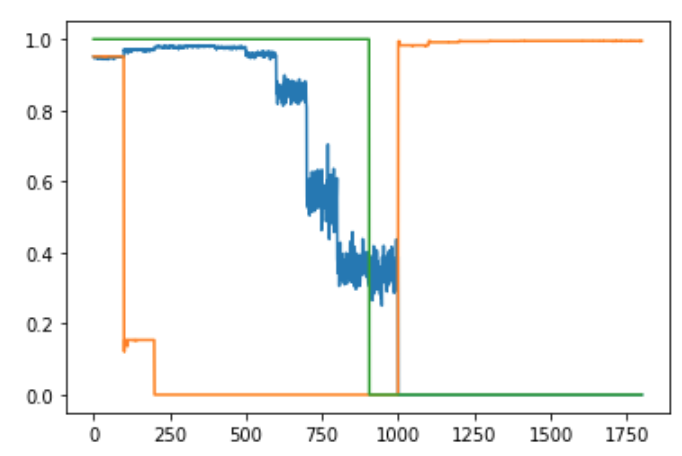
This plot shows the mask output over an epoch. The blue and the orange lines are the mask output to the two nodes of the target layer. The green line is the class label. The lines look piece-wise horizontal because the data are seen in batches, but plotted sequentially. It looks like one of the nodes is turned off (with mask=0) almost entirely for the first class label seen, and then turned on later to learned the second class. The other node is used for the first class, and later turned off when the second class shows up.
This is quite an interesting behavior. My hypothesis is that a node is turned off for the first class so that the weights stays close to initialization, and it’s easier to learn a new class from initialization than to have to unlearn a previously learned task.
I’m still working on more followup experiments and extending to more complex scenarios; will post more when there’re more interesting results.
